Ley de los grandes números Índice Historia Ley débil Ley fuerte Véase también Referencias Menú de...
Teoría estadísticaTeoremas de probabilidadDemostraciones matemáticasCiencia de 1713Ciencia y tecnología de SuizaTeoremas de la teoría de las probabilidades
teoría de la probabilidadteoremaspromediosucesiónvariables aleatoriasconverjaesperanzaspoblaciónvarianzateorema central del límitevariable aleatoria normalGerolamo CardanoJacob BernoulliDaniel BernoulliS.D. PoissonChebyshevMarkovBorelCantelliKolmogorovKhinchinvariables arbitrariasvalor esperadovarianzaconverge en probabilidadcasi seguramentelema de Borel-Cantellidesigualdad de Chebyshev
En la teoría de la probabilidad, bajo el término genérico de ley de los grandes números se engloban varios teoremas que describen el comportamiento del promedio de una sucesión de variables aleatorias conforme aumenta su número de ensayos.
Estos teoremas prescriben condiciones suficientes para garantizar que dicho promedio converja (en los sentidos explicados abajo) al promedio de las esperanzas de las variables aleatorias involucradas. Las distintas formulaciones de la ley de los grandes números (y sus condiciones asociadas) especifican la convergencia de formas distintas.
Las leyes de los grandes números explican por qué el promedio de una muestra al azar de una población de gran tamaño tenderá a estar cerca de la media de la población completa...
Cuando las variables aleatorias tienen una varianza finita, el teorema central del límite extiende nuestro entendimiento de la convergencia de su promedio describiendo la distribución de diferencias estandarizadas entre la suma de variables aleatorias y el valor esperado de esta suma: sin importar la distribución subyacente de las variables aleatorias, esta diferencia estandarizada converge a una variable aleatoria normal estándar.
La frase "ley de los grandes números" es también usada ocasionalmente para referirse al principio de que la probabilidad de que cualquier evento posible (incluso uno improbable) ocurra al menos una vez en una serie aumenta con el número de eventos en la serie. Por ejemplo, la probabilidad de que un individuo gane la lotería es bastante baja; sin embargo, la probabilidad de que alguien gane la lotería es bastante alta, suponiendo que suficientes personas comprasen boletos de lotería.
Índice
1 Historia
2 Ley débil
3 Ley fuerte
4 Véase también
5 Referencias
Historia
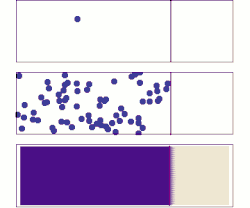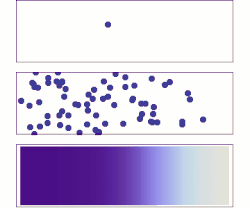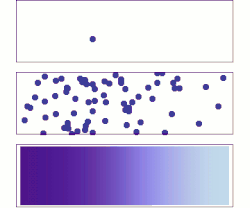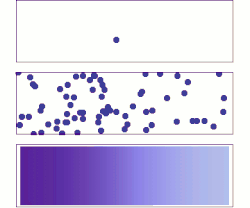
La difusión es un ejemplo de la ley de los grandes números, aplicada a la química. Inicialmente, hay moléculas de soluto en el lado izquierdo de una barrera (línea púrpura) y ninguna a la derecha. Se elimina la barrera y el soluto se difunde para llenar todo el contenedor.
Arriba: con una sola molécula, el movimiento parece ser bastante aleatorio.
Medio: con más moléculas, existe una clara tendencia en la que el soluto llena el recipiente más y más uniformemente, pero también hay fluctuaciones.
Abajo: con un enorme número de moléculas de soluto (demasiadas para verse), la aleatoriedad esencialmente desaparece: el soluto parece moverse suave y sistemáticamente desde las zonas de alta concentración a las zonas de baja concentración. En situaciones reales, los químicos pueden describir la difusión como un fenómeno macroscópico determinista (ver leyes de Fick), a pesar de su carácter aleatorio subyacente.
El matemático italiano Gerolamo Cardano (1501–1576) afirmó sin pruebas que la precisión de las estadísticas empíricas tienden a mejorar con el número de intentos.[1] Después esto fue formalizado como una ley de los grandes números. Una forma especial de la ley (para una variable aleatoria binaria) fue demostrada por primera vez por Jacob Bernoulli.[2] Le llevó más de 20 años desarrollar una prueba matemática suficientemente rigurosa que fue publicada en su Ars Conjectandi [El arte de la conjetura] en 1713. Bernouilli le llamó su «Teorema dorado», pero llegó a ser conocido generalmente como «teorema de Bernoulli". Este no debe confundirse con el principio físico de igual nombre, el nombre del sobrino de Jacob, Daniel Bernoulli. En 1837, S.D. Poisson describió con más detalle bajo el nombre de «la loi des grands nombres» (la ley de los grandes números).[3][4] A partir de entonces, se conoce con ambos nombres, pero se utiliza con mayor frecuencia la «ley de los grandes números».
Después de que Bernoulli y Poisson publicasen sus esfuerzos, otros matemáticos también contribuyeron al refinamiento de la ley, como Chebyshev,[5] Markov, Borel, Cantelli y Kolmogorov y Khinchin, que finalmente proporcionó una prueba completa de la ley de los grandes números para variables arbitrarias.[6] Estos nuevos estudios han dado lugar a dos formas prominentes de la ley de los grandes números: una se llama la ley "débil" y la otra la ley "fuerte", en referencia a dos modos diferentes de convergencia de la muestra acumulada significa el valor esperado; en particular, como se explica a continuación, la forma fuerte implica la débil.[6]
Ley débil
La ley débil de los grandes números establece que si X1, X2, X3, ... es una sucesión infinita de variables aleatorias independientes que tienen el mismo valor esperado μ{displaystyle mu } y varianza σ2{displaystyle sigma ^{2}}, entonces el promedio
- X¯n=(X1+⋯+Xn)/n{displaystyle {overline {X}}_{n}=(X_{1}+cdots +X_{n})/n}
converge en probabilidad a μ. En otras palabras, para cualquier número positivo ε se tiene
- limn→∞P(|X¯n−μ|<ε)=1.{displaystyle lim _{nrightarrow infty }operatorname {P} left(left|{overline {X}}_{n}-mu right|<varepsilon right)=1.}
Ley fuerte
La ley fuerte de los grandes números establece que si X1, X2, X3, ... es una sucesión infinita de variables aleatorias independientes e idénticamente distribuidas que cumplen E(|Xi|) < ∞ y tienen el valor esperado μ, entonces
- P(limn→∞X¯n=μ)=1,{displaystyle operatorname {P} left(lim _{nrightarrow infty }{overline {X}}_{n}=mu right)=1,}
es decir, el promedio de las variables aleatorias converge a μ casi seguramente (en un conjunto de probabilidad 1).
Esta ley justifica la interpretación intuitiva del valor esperado de una variable aleatoria como el "promedio a largo plazo al hacer un muestreo repetitivo".
Para demostrar el teorema haremos uso del siguiente lema:
Desigualdad Maximal. Sean Z1,...,ZN{displaystyle Z_{1},...,Z_{N},} variables aleatorias independientes y sean ϵ1,ϵ2{displaystyle epsilon _{1},,,epsilon _{2}} y β{displaystyle beta ,!} constantes positivas que cumplen P{|Zi+Zi+1+...+ZN|≤ϵ2}≥1/β{displaystyle mathbb {P} {|Z_{i}+Z_{i+1}+...+Z_{N}|leq epsilon _{2}}geq 1/beta } para cada i. Luego
- P{maxi≤N|Z1+...+Zi|>ϵ1+ϵ2}≤βP{|Z1+...+ZN|>ϵ1}{displaystyle mathbb {P} {max_{ileq N}|Z_{1}+...+Z_{i}|>epsilon _{1}+epsilon _{2}}leq beta mathbb {P} {|Z_{1}+...+Z_{N}|>epsilon _{1}}}
Demostración del lema: Sean Si:=Z1+...+Zi{displaystyle S_{i}:=Z_{1}+...+Z_{i},} y Ti:=SN−Si{displaystyle T_{i}:=S_{N}-S_{i},}. Definamos asimismo la variable aleatoria
τ={primer i para el cual |Si|>ϵ1+ϵ2Nsi |Si|≤ϵ1+ϵ2para todo i{displaystyle tau =left{{begin{matrix}{text{primer i para el cual }}|S_{i}|>epsilon _{1}+epsilon _{2}\N,,{text{si }}|S_{i}|leq epsilon _{1}+epsilon _{2},,{text{para todo }}iend{matrix}}right.}
Tenemos entonces:
- P{maxi≤N|Z1+...+Zi|>ϵ1+ϵ2}=P{τ=i,|Si|>ϵ1+ϵ2 para algun i}=∑i=1NP{τ=i,|Si|>ϵ1+ϵ2}pues son eventos disjuntos≤∑i=1NP{τ=i,|Si|>ϵ1+ϵ2}βP{|Ti|≤ϵ2}hipotesis del lema=β∑i=1NP{τ=i,|Si|>ϵ1+ϵ2,|Ti|≤ϵ2}por independencia entre los Si y los Ti{displaystyle {begin{array}{rcl}mathbb {P} {max_{ileq N}|Z_{1}+...+Z_{i}|>epsilon _{1}+epsilon _{2}}&=&mathbb {P} {tau =i,|S_{i}|>epsilon _{1}+epsilon _{2}{text{ para algun i}}}\&=&sum _{i=1}^{N}mathbb {P} {tau =i,|S_{i}|>epsilon _{1}+epsilon _{2}}quad {text{pues son eventos disjuntos}}\&leq &sum _{i=1}^{N}mathbb {P} {tau =i,|S_{i}|>epsilon _{1}+epsilon _{2}}beta mathbb {P} {|T_{i}|leq epsilon _{2}}quad {text{hipotesis del lema}}\&=&beta sum _{i=1}^{N}mathbb {P} {tau =i,|S_{i}|>epsilon _{1}+epsilon _{2},|T_{i}|leq epsilon _{2}}quad {text{por independencia entre los }}S_{i}{text{ y los }}T_{i}end{array}}}
Ahora bien, si |Si|>ϵ1+ϵ2{displaystyle |S_{i}|>epsilon _{1}+epsilon _{2},} y |Ti|≤ϵ2{displaystyle |T_{i}|leq epsilon _{2}} entonces implica que
|Si|>ϵ1{displaystyle |S_{i}|>epsilon _{1},} por ende:
- P{maxi≤N|Z1+...+Zi|>ϵ1+ϵ2}≤β∑i=1NP{τ=i,|Si|>ϵ1}=βP{|Z1+...+ZN|>ϵ1}{displaystyle mathbb {P} {max_{ileq N}|Z_{1}+...+Z_{i}|>epsilon _{1}+epsilon _{2}}leq beta sum _{i=1}^{N}mathbb {P} {tau =i,|S_{i}|>epsilon _{1}}=beta mathbb {P} {|Z_{1}+...+Z_{N}|>epsilon _{1}}}
con lo que se concluye el lema. (Fin demostración del lema)
Sigamos con la demostración del teorema: Definamos
- Si:=X1+...+Xiσi2:=PXi2;Vi:=σ12+...+σi2=PSi2Bk:=n:nk<n≤nk+1donde nk:=2k,k=1,2,3,...{displaystyle {begin{array}{rcl}S_{i}&:=&X_{1}+...+X_{i}\sigma _{i}^{2}&:=&mathbb {P} X_{i}^{2},;quad V_{i}:=sigma _{1}^{2}+...+sigma _{i}^{2}=mathbb {P} S_{i}^{2}\B_{k}&:=&{n:n_{k}<nleq n_{k+1}}quad {text{donde }}n_{k}:=2^{k},,,k=1,2,3,...end{array}}}
Tenemos entonces que la serie ∑kV(nk)/nk2{displaystyle sum _{k}V(n_{k})/n_{k}^{2}} es convergente pues:
- ∑k=1∞V(nk)/nk2=∑k=1∞∑j=1∞σj2χ{j≤2k}4−k=∑j=1∞σj2∑k=1∞χ{j≤2k}4−k=∑j=1∞σj24−([log2j]+1)43≤43∑j=1∞σj2/j2<∞{displaystyle sum _{k=1}^{infty }V(n_{k})/n_{k}^{2}=sum _{k=1}^{infty }sum _{j=1}^{infty }sigma _{j}^{2}chi _{{jleq 2^{k}}}4^{-k}=sum _{j=1}^{infty }sigma _{j}^{2}sum _{k=1}^{infty }chi _{{jleq 2^{k}}}4^{-k}=sum _{j=1}^{infty }sigma _{j}^{2}4^{-([log _{2}j]+1)}{frac {4}{3}}leq {frac {4}{3}}sum _{j=1}^{infty }sigma _{j}^{2}/j^{2}<infty }
![{displaystyle sum _{k=1}^{infty }V(n_{k})/n_{k}^{2}=sum _{k=1}^{infty }sum _{j=1}^{infty }sigma _{j}^{2}chi _{{jleq 2^{k}}}4^{-k}=sum _{j=1}^{infty }sigma _{j}^{2}sum _{k=1}^{infty }chi _{{jleq 2^{k}}}4^{-k}=sum _{j=1}^{infty }sigma _{j}^{2}4^{-([log _{2}j]+1)}{frac {4}{3}}leq {frac {4}{3}}sum _{j=1}^{infty }sigma _{j}^{2}/j^{2}<infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f7cd4f791805a6ef89c4e7e9350ce0675a3fcf2)
La convergencia c.t.p. que asegura el teorema es equivalente a:
- maxn|Sn|n→0cuando k→∞{displaystyle max _{n}{frac {|S_{n}|}{n}}rightarrow 0quad {text{cuando }}krightarrow infty }
Por el lema de Borel-Cantelli, es suficiente demostrar que, para todo ϵ>0{displaystyle epsilon >0,!}
( 1)∑kP{maxn∈Bk|Sn|n>ϵ}<∞{displaystyle sum _{k}mathbb {P} left{max _{nin B_{k}}{frac {|S_{n}|}{n}}>epsilon right}<infty }
Cada probabilidad en la suma anterior puede ser acotada por:
- P{maxn≤nk+1|Sn|>ϵnk}{displaystyle mathbb {P} left{max _{nleq n_{k+1}}|S_{n}|>epsilon n_{k}right}}
Ahora se aplica la desigualdad maximal:
- P{maxn≤nk+1|Sn|>ϵnk}≤βkP{|Snk+1|>ϵ2nk}≤βk4V(nk+1)/(ϵnk)2{displaystyle mathbb {P} left{max _{nleq n_{k+1}}|S_{n}|>epsilon n_{k}right}leq beta _{k}mathbb {P} {|S_{n_{k+1}}|>{frac {epsilon }{2}},n_{k}}leq beta _{k}4V(n_{k+1})/(epsilon n_{k})^{2}}
La última desigualdad de la línea anterior se justifica por la desigualdad de Chebyshev. Una nueva aplicación de esta misma desigualdad nos permite acotar los βk{displaystyle beta _{k},}:
- βk−1=minn≤nk+1P{|Snk+1−Sn|≤ϵ2nk}≥1−maxn≤nk+14P(Snk+1−Sn)2ϵ2nk2≥1−16V(nnk+1)ϵ2nk2→1cuando k→∞{displaystyle {begin{array}{rcl}beta _{k}^{-1}&=&min _{nleq n_{k+1}}mathbb {P} {|S_{n_{k+1}}-S_{n}|leq {frac {epsilon }{2}}n_{k}}\&geq &1-max _{nleq n_{k+1}}{frac {4mathbb {P} (S_{n_{k+1}}-S_{n})^{2}}{epsilon ^{2}n_{k}^{2}}}\&geq &1-{frac {16,V(n_{n_{k}+1})}{epsilon ^{2}n_{k}^{2}}}rightarrow 1qquad {text{cuando }}krightarrow infty end{array}}}
Es decir, hemos logrado acotar cada sumando de la () por una constante por los términos de una sumatoria que sabemos convergente, demostrando la convergencia de dicha sumatoria y concluyendo via Borel-Cantelli la convergencia fuerte del teorema.
(Fin de la demostración)◼{displaystyle blacksquare }
Definamos Yi=Xiχ{|Xi|≤i}{displaystyle Y_{i}=X_{i}chi _{{|X_{i}|leq i}},} y μi=PYi{displaystyle mu _{i}=mathbb {P} Y_{i},}. Tenemos que 0=PXi=μi+PXiχ{|Xi|>i}{displaystyle 0=mathbb {P} X_{i}=mu _{i}+mathbb {P} X_{i}chi _{{|X_{i}|>i}}}. Además, usando la hipótesis de distribuciones idénticas, podemos en general reemplazar (no siempre) una distribución Xi{displaystyle X_{i},} genérica por un representante, digamos X1{displaystyle X_{1},}. Tenemos entonces:
(1)|1n∑i≤nμi|≤P1n∑i≤n|X1|χ{|X1|>i}≤P{|X1|min(1,|X1|n)}→0{displaystyle left|{frac {1}{n}}sum _{ileq n}mu _{i}right|leq mathbb {P} {frac {1}{n}}sum _{ileq n}|X_{1}|chi _{{|X_{1}|>i}}leq mathbb {P} left{|X_{1}|min left(1,{frac {|X_{1}|}{n}}right)right}rightarrow 0}
La última convergencia a cero viene dada por la convergencia puntual más convergencia dominada por |X1|{displaystyle ,|X_{1}|} .
También tenemos que:
(2)∑i=1∞P{Xi≠Yi}=∑i=1∞P{|Xi|>i}=∑i=1∞P{|X1|>i}=∑i=1∞iP{|X1|>i,|X1|≤i+1}≤P|X1|<∞{displaystyle {begin{array}{rcl}sum _{i=1}^{infty }mathbb {P} {X_{i}neq Y_{i}}&=&sum _{i=1}^{infty }mathbb {P} {|X_{i}|>i}\&=&sum _{i=1}^{infty }mathbb {P} {|X_{1}|>i}\&=&sum _{i=1}^{infty }i,mathbb {P} {{|X_{1}|>i,|X_{1}|leq i+1}}\&leq &mathbb {P} |X_{1}|<infty end{array}}}
La tercera igualdad viene de que para cualquier variable aleatoria se cumple que:
- ∑i≥1χ{X>i}=∑i≥1iχ{X>i,x≤i+1}{displaystyle sum _{igeq 1}chi _{{X>i}}=sum _{igeq 1}i,chi _{{X>i,xleq i+1}}}
La () implica, por Borel-Canteli, que el conjunto {Xi≠Yi,para infinitos i}{displaystyle {X_{i}neq Y_{i},,{text{para infinitos i}}}} tiene probabilidad cero. Por lo tanto, en un conjunto de probabilidad 1 se cumple:
(3)|1n∑i≤nXi−1n∑i≤nYi|→0{displaystyle left|{frac {1}{n}}sum _{ileq n}X_{i}-{frac {1}{n}}sum _{ileq n}Y_{i}right|rightarrow 0}
De la desigualdad P(Yi−μi)2≤PYi2=P(X12χ{|X1|≤i}){displaystyle mathbb {P} (Y_{i}-mu _{i})^{2}leq mathbb {P} Y_{i}^{2}=mathbb {P} (X_{1}^{2}chi _{{|X_{1}|leq i}}),} podemos deducir que:
- ∑i=1∞P(Yi−μi)2i2≤∑i=1∞P(X12χ{|X1|≤i})i2=P{∑i=1∞X12χ{|X1|≤i}i2}≤CP|X1|<∞{displaystyle sum _{i=1}^{infty }{frac {mathbb {P} (Y_{i}-mu _{i})^{2}}{i^{2}}}leq sum _{i=1}^{infty }{frac {mathbb {P} (X_{1}^{2}chi _{{|X_{1}|leq i}})}{i^{2}}}=mathbb {P} left{sum _{i=1}^{infty }{frac {X_{1}^{2}chi _{{|X_{1}|leq i}}}{i^{2}}}right}leq Cmathbb {P} |X_{1}|<infty }
Por el teorema anteriormente demostrado tenemos:
(4)1n∑i≤n(Yi−μi)→0{displaystyle {frac {1}{n}}sum _{ileq n}(Y_{i}-mu _{i})rightarrow 0}
casi seguramente. Como además tenemos que:
- |1n∑i≤nXi|≤|1n∑i≤n(Xi−Yi)|+|1n∑i≤n(Yi−μi)|+|1n∑i≤nμi|{displaystyle left|{frac {1}{n}}sum _{ileq n}X_{i}right|leq left|{frac {1}{n}}sum _{ileq n}(X_{i}-Y_{i})right|+left|{frac {1}{n}}sum _{ileq n}(Y_{i}-mu _{i})right|+left|{frac {1}{n}}sum _{ileq n}mu _{i}right|}
Entonces, de las ecuaciones (), () y () se deduce que |1n∑i≤nXi|→0{displaystyle left|{frac {1}{n}}sum _{ileq n}X_{i}right|rightarrow 0,} en casi en todos los puntos, concluyendo el teorema.
(Fin de la demostración)◼{displaystyle blacksquare }
Véase también
- Teorema central del límite
- Teorema de Bernoulli
- Falacia del jugador
- Andréi Kolmogórov
- Ley de los números realmente grandes
Referencias
- David Pollard, A user´s guide to measure theoretic probability, Cambridge University Press (2003).
↑ Mlodinow, L. The Drunkard's Walk. New York: Random House, 2008. p. 50.
↑ Jakob Bernoulli, Ars Conjectandi: Usum & Applicationem Praecedentis Doctrinae in Civilibus, Moralibus & Oeconomicis, 1713, Chapter 4, (Translated into English by Oscar Sheynin)
↑ Poisson names the "law of large numbers" (la loi des grands nombres) in: S.D. Poisson, Probabilité des jugements en matière criminelle et en matière civile, précédées des règles générales du calcul des probabilitiés (Paris, France: Bachelier, 1837), p. 7. He attempts a two-part proof of the law on pp. 139–143 and pp. 277 ff.
↑ Hacking, Ian. (1983) "19th-century Cracks in the Concept of Determinism", Journal of the History of Ideas, 44 (3), 455-475
↑ Tchebichef, P. (1846). «Démonstration élémentaire d'une proposition générale de la théorie des probabilités». Journal für die reine und angewandte Mathematik (Crelles Journal) 1846 (33): 259-267. doi:10.1515/crll.1846.33.259.
↑ ab Seneta, 2013.
