Base ortonormal Índice Definiciones Ejemplos Consecuencias Construcción Referencias Menú de...
Álgebra linealAnálisis funcional
álgebra linealespacio prehilbertianoespacio vectorialproducto internoespacio de Hilbertspanortogonalesescalarbaseortogonalnormaálgebra linealcombinación linealproducto internoEspacio de Banachespacio de Hilbertbase canónicanormaproducto interno∎intervaloseries de Fourierdefinición del producto internosistema de coordenadas ortogonallema de Zornproceso de Gram-Schmidtvectores unitarios
Base ortonormal del plano euclídeo.
En álgebra lineal, una base ortonormal de un espacio prehilbertiano V (es decir, un espacio vectorial con producto interno) o, en particular, de un espacio de Hilbert H, es un conjunto de elementos cuyo span es denso en el espacio, en el que los elementos son mutuamente ortogonales y normales, es decir, de magnitud unitaria. Una base ortogonal satisface las mismas condiciones, salvo la de magnitud unitaria; es muy sencillo transformar una base ortogonal en una base ortonormal mediante el producto por un escalar apropiado y de hecho, esta es la forma habitual en la que se obtiene una base ortonormal: por medio de una base ortogonal.
Así, una base ortonormal es una base ortogonal, en la cual la norma de cada elemento que la compone es unitaria.
Estos conceptos son importantes tanto para espacios de dimensión finita como de dimensión infinita. Para espacios de dimensión finita, la condición de span denso es la misma que la de 'span', como se usa en álgebra lineal.
Una base ortonormal por lo general no es una "base", es decir, en general no es posible escribir a cada elemento del espacio como una combinación lineal de un número finito de elementos de la base ortonormal. En el caso de dimensión infinita, esta distinción cobra importancia: la definición dada requiere solo que el generado de una base ortonormal sea densa en el espacio vectorial, y no que iguale al espacio entero.
Una base ortonormal de un espacio vectorial V no tiene sentido si el espacio no posee un producto interno. Un Espacio de Banach no tendrá una base ortonormal a no ser que sea un espacio de Hilbert.
Índice
1 Definiciones
2 Ejemplos
3 Consecuencias
4 Construcción
5 Referencias
Definiciones
Sea (V,⟨⋅,⋅⟩){displaystyle left(V,leftlangle cdot ,cdot rightrangle right)} un espacio prehilbertiano de dimensión finita n.
|
Un conjunto de vectores ortonormales que engendran V constituyen una base para V, la cual es llamada base ortonormal.[1]
Ejemplos
El conjunto {e1, e2, e3} con
{e1=(1,0,0)e2=(0,1,0)e3=(0,0,1){displaystyle left{{begin{array}{rcl}e_{1}&=&(1,0,0)\e_{2}&=&(0,1,0)\e_{3}&=&(0,0,1)end{array}}right.}
es decir la base canónica forma una base ortonormal de R3.
Demostración
Mediante un cálculo directo se verifica que
- ⟨e1,e2⟩=⟨e1,e3⟩=⟨e2,e3⟩=0{displaystyle leftlangle e_{1},e_{2}rightrangle =leftlangle e_{1},e_{3}rightrangle =leftlangle e_{2},e_{3}rightrangle =0}
y que
- ‖e1‖=‖e2‖=‖e3‖=1{displaystyle left|e_{1}right|=left|e_{2}right|=left|e_{3}right|=1}
siendo ‖x‖=⟨x,x⟩{displaystyle scriptstyle |x|={sqrt {leftlangle x,xrightrangle }}} la norma inducida por el producto interno.
Así, {e1, e2, e3} es un conjunto ortonormal. Para un (x,y,z) cualquiera en R3 tenemos
- (x,y,z)=xe1+ye2+ze3,{displaystyle (x,y,z)=xe_{1}+ye_{2}+ze_{3},,}
entonces, {e1,e2,e3} reconstruye R3 y por lo tanto tiene que ser una base∎
También puede demostrarse que la base estándar, rotada alrededor de un eje que pasa por el origen, o reflejada en un plano que pasa por el origen, forma también una base ortonormal de R3.
Base ortonormal de funciones trigonométricas.
El conjunto {fn : n ∈ N} con
fn:R⟶R,fn(x)=cos{[2n−1+(−1)n4]2πx−[1+(−1)n]π4}{displaystyle {begin{array}{rl}f_{n}:&mathbb {R} longrightarrow mathbb {R} ,\f_{n}(x)=&cos left{left[{frac {2n-1+(-1)^{n}}{4}}right]2pi x-left[1+(-1)^{n}right]{frac {pi }{4}}right}end{array}}}
es decir, la sucesión infinita de funciones
- 1, sen(2πx), cos(2πx), sen(4πx), cos(4πx), sen(6πx), cos(6πx), ...
forma una base ortogonal del espacio de funciones reales cuadrado integrables en el intervalo [0, 1].
Sea an : N → {1/2, 1} la sucesión definida por
- an={1 si n=112 si n>1{displaystyle a_{n}={begin{cases}1&{text{ si }}n=1\{frac {1}{2}}&{text{ si }}n>1end{cases}}}
entonces el conjunto G = {gn : n ∈ N}, con
gn:R⟶R,gn(x)=anfn(x){displaystyle {begin{array}{rl}g_{n}:&mathbb {R} longrightarrow mathbb {R} ,\g_{n}(x)=&a_{n}f_{n}(x)end{array}}}
forma una base ortonormal de dicho espacio.
El conjunto {fn : n ∈ Z} con
fn:R⟶C,fn(x)=e2πinx{displaystyle {begin{array}{rl}f_{n}:&mathbb {R} longrightarrow mathbb {C} ,\f_{n}(x)=&e^{2pi inx}end{array}}}
forma una base ortogonal del espacio complejo L2([0,1]). Este es un resultado fundamental para el estudio de series de Fourier.
El conjunto {eb : b ∈ B} con
eb(c)={1si b=c0si b≠c{displaystyle e_{b}(c)={begin{cases}1&{textrm {si}} b=c\0&{textrm {si}} bneq cend{cases}}}
forma una base ortonormal de l2(B).
Eigenfunciones de un problema de Sturm-Liouville.
![{displaystyle {begin{array}{rl}f_{n}:&mathbb {R} longrightarrow mathbb {R} ,\f_{n}(x)=&cos left{left[{frac {2n-1+(-1)^{n}}{4}}right]2pi x-left[1+(-1)^{n}right]{frac {pi }{4}}right}end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/075fee1ff8c73ec3af1d55bcd75ab228dbe067c7)
Consecuencias
Si un espacio prehilbertiano (V,⟨⋅,⋅⟩){displaystyle left(V,leftlangle cdot ,cdot rightrangle right)} posee una base ortonormal E={e1,e2,…,en}{displaystyle E=left{e_{1},e_{2},dots ,e_{n}right}} finita, cada vector x en V puede expresarse de la siguiente manera:
x=∑i=1n⟨x,ei⟩ei{displaystyle mathbf {x} =sum _{i=1}^{n}leftlangle x,e_{i}rightrangle e_{i}}
Demostración |
Sean xi las coordenadas del vector x en a base E, por definición
Se escoge un vector ej del conjunto E para calcular el producto interno entre este vector y x:
La definición del producto interno permite «extraer» las combinaciones lineales, con lo cual
pero como la base es ortonormal
de donde se deduce que ⟨x,ej⟩=xj{displaystyle scriptstyle leftlangle mathbf {x} ,e_{j}rightrangle =x_{j}}∎ |
En términos no tan formales, la expresión describe el hecho de que las coordenadas de un vector en un sistema de coordenadas ortogonal consisten en la magnitud de la proyección del vector sobre cada uno de los ejes que componen al sistema.
Construcción
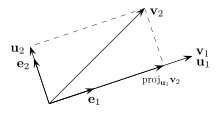
Ilustración del proceso de Gram-Schmidt para una base no ortogonal {v1, v2} de R2.
Para espacios de dimensión finita, conocido es el teorema que reza lo siguiente.
|
Sea (V,⟨⋅,⋅⟩){displaystyle left(V,leftlangle cdot ,cdot rightrangle right)} un espacio de este tipo, y sea n su dimensión. Selecciónese una base
- B={v1,v2,…,vn}.{displaystyle {mathcal {B}}=left{v_{1},v_{2},dots ,v_{n}right}.}
cuya existencia está asegurada por el lema de Zorn. Los vectores de la base no son, necesariamente, unitarios ni ortogonales entre sí. Para poder construir una base ortonormal a partir de la base dada, puede utilizarse el proceso de Gram-Schmidt.
Dicho proceso consiste básicamente en
- escoger arbitrariamente un par de vectores de B{displaystyle {mathcal {B}}}, por ejemplo v1 y v2.
- Calcular la proyección ortogonal de v2 sobre v1. La diferencia entre v2 y el vector resultante es ortogonal a v1.
- Tomar otro vector v3 y calcular su proyección ortogonal sobre el subespacio vectorial de V generado por v1 y v2. La diferencia entre v3 y la referida proyección es ortogonal a v1 y v2.
- Se sigue el proceso de la misma manera con v4, v5, ... vn hasta obtener una base ortogonal de V.
Por comodidad de cálculo, suelen emplearse las designaciones siguientes.
- {u1=v1uk=vk−∑j=1k−1Proyvj(uj)para 1≤k≤n.{displaystyle left{{begin{array}{rcll}u_{1}&=&v_{1}&\u_{k}&=&v_{k}-displaystyle sum _{j=1}^{k-1}operatorname {Proy} _{v_{j}}left(u_{j}right)&{textrm {para}} 1leq kleq n.end{array}}right.}
El proceso de ortogonalización provee la base {u1, u2, ... , un} compuesta por n vectores ortogonales entre sí. Basta entonces elegir el conjunto {e1, e2, ... , en} compuesto por los vectores unitarios definidos por
- ek=uk‖uk‖,para 1≤k≤n{displaystyle e_{k}={frac {u_{k}}{left|u_{k}right|}},quad {textrm {para}} 1leq kleq n}
para obtener la tesis del teorema.
Referencias
↑ Birkhoff, Saunders; MacLane (1963). Álgebra Moderna (1ª edición). España: Vicens - Vivens. p. 201.
↑
Selzer, Samuel. Álgebra y geometría analítica (2ª edición). Buenos Aires: Nigar. p. 466.
