Sfrgttk

En geometría se denomina lúnula a cualquiera de las dos figuras con forma semejante a la de una luna creciente obtenidas mediante la intersección de dos círculos.

La palabra lúnula deriva del latín lunŭla, diminutivo de luna.^[1]​

Geometría plana

En geometría plana una lúnula es un área cóncava limitada por dos arcos. La correspondiente forma convexa se denomina lente.

Formalmente, una lúnula es el complemento de un círculo en otro, situados de forma que ambos se intersecan, pero ninguno es un subconjunto del otro.^[2]​ Esto es, si A y B son dos círculos, entonces:

L=A−A∩B{displaystyle L=A-Acap B}

es una lúnula. Si A es el círculo de la derecha:

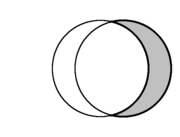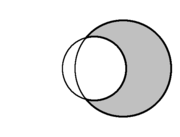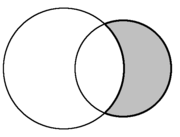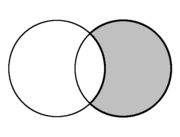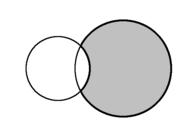En geometría del plano, la forma creciente formada por la intersección de dos círculos se denomina lúnula (resaltada en gris).

Geometría esférica

Una lúnula esférica o huso. Los dos círculos grandes se muestran como líneas negras finas, mientras que la lúnula esférica o huso (en verde) está perfilada con líneas negras gruesas, correspondiendo a sus medias circuferencias máximas generadoras. Estas circuferencias máximas definen otros tres husos, y se intersecan en dos puntos polares opuestos, como en el caso de los polos Norte y Sur geométricos.

En geometría esférica, una lúnula ^[3]​ es un área de una esfera limitada por la mitad de dos circunferencias máximas,^[4]​ también denominada huso^[5]​ (en inglés digon o diangle, en alemán Kugelzweieck). Las circuferencias máximas son las de mayor radio posible sobre una esfera: cada circuferencia máxima divide la superficie de la esfera en dos mitades iguales. Dos circuferencias máximas se intersecan siempre en dos puntos opuestos.

Ejemplos comunes de circuferencias máximas son las líneas de longitud (meridianos), que se cruzan en los polos Norte y Sur geométricos. El área entre dos meridianos de longitud es un huso.

El área de un huso esférico se calcula mediante la fórmula:

S=2θR2 {displaystyle S=2theta R^{2} }

donde R es el radio de la esfera, y θ es el ángulo diedro entre las dos medias circuferencias máximas.^[6]​

Cuando este ángulo θ es 2π, esto es, cuando la segunda circuferencia se ha movido una circunferencia entera y el huso entre ellas cubre por completo a la esfera, la fórmula del área del huso vale 4πR²: la superficie de la esfera.

La luna creciente es un huso, tal como se describe en el texto. Aquí, las porciones roja y azul pueden ser tomadas como las porciones iluminada y oscura de la Luna tal como se ven desde la Tierra, o viceversa.

La parte iluminada de la Luna tiene también forma de huso. La primera de las dos circunferencias máximas es el límite que separa las partes iluminada y no iluminada de la Luna. La segunda circunferencia es la que separa la mitad de la Luna visible desde la Tierra de la que no lo es. Vista de frente, este huso iluminado tiene la forma familiar de una luna creciente (o decreciente) vista desde la Tierra, como se ilustra en la figura de la derecha.

Véase también

• Cuadratura de la lúnula


• Hipócrates de Quíos


• Geometría esférica


• Teorema de Gauss-Bonnet


• Círculo máximo

Referencias

Enlaces externos

• 
  Wikimedia Commons alberga una categoría multimedia sobre Lúnula.


• 
  Las cinco lúnulas cuadrables en MathPages.com (en inglés).